Capítulo 4 Manipulación de datos

Functional programming combines the flexibility and power of abstract mathematics with the intuitive clarity of abstract mathematics. Randall Munroe

4.1 Introducción

El manejo de datos es una de las actividades que más tiempo insumen en el análisis cuantitativo cuantitiva. Manejar datos significa cambiarles la forma, aplicándoles tranformaciones, hasta llevarlos a la estructura necesaria para el análisis que queremos llevar a cabo. ¿Cuál es la “estructura necesaria”? La respuesta dependerá de lo que estemos haciendo en dos sentidos diferentes. El primero es de naturaleza técnica y se vincula con los requisitos de input de las funciones de R. El segundo tiene que ver con nuestros intereses de investigación.

En términos estríctamente técnicos y desde el punto de vista del procesamiento de datos con R generalmente quiere decir que hemos creado una estructura de datos que tiene las características requeridas por alguna función de análisis que queremos aplicar, por ejemplo, un modelo lineal. Los modelos lineales en R requieren que nuestros datos tenga la estructura data.frame o asimilable, que las columnas tengan el tipo adecuado –numéricas si estamos haciendo un OLS, factores si estamos ajustando un modelo generalizado-, que los nombres sean válidos y que no haya casos perdidos. Esas características suelen estar especificadas en la ayuda de las funciones y se describen bajo el rótulo data o x.

La ayuda de la función sd() señala que el argumento x con el que pasamos los datos sobre los que se calculará la desviación estándar debe ser un vector numérico o un objeto que pueda convertirse en un vector numérico. Si en los datos con los que comenzamos no cumplen con este requisito –por ejemplo, son del tipo caractér- debemos transformarlos previamente.

En término sustantivos la estructura necesaria de nuestros datos depende de nuestra pregunta de investigación y nuestra unidad de análisis. La estructura de los datos que analizamos debe ser consistente, no podría analizar el comportamiento de cierta variable a nivel Estados cuando los datos que tengo son a nivel nacional. Del mismo modo, si me interesan una variable a nivel nacional y dispongo de datos a nivel sub-nacional será necesario agregar los datos hasta llevarlos a la unidad de análisis que me interesa7. Si mi base de datos incluye información sobre todos los países del mundo deberé filtrarlos, si tiene errores de ortografía o códigos inconvenientes o inconsistentes será necesario recodificarlas. Si esto fuera poco nuestra pregunta de investigación puede requerir datos que no están juntos de antemano y necesitemos unir bases de datos.

Si bien estos dos sentidos de “manejo” de datos y los objetivos de cada uno son muy diferentes, trivial en el primer caso, muy complejo en el segundo, los aquí se presentan unidos en un capítulo. La razón es que, aunque los objetivos son distintos y las decisiones que tomemos estarán orientadas en un caso a resolver un problema técnico y en el otro uno de investigación, las herramientamos que utilizamos son las mismas.

En este capítulo se presentan algunas herramientas básicas para dar una forma manejable a los datos y luego transformarlos. Más importante que estas herramientas son los conceptos que se presentarán y estos serán de utilidad independientemente de que el trabajo de organización y manejo de datos se haga en R, en Stata o en Excel.8 El primer concepto es pensar a los datos como una serie de estados más que como una cosa. El manejo de datos consisten en ir cambiando de manera controlada esos estados hasta llegar al que nos interesa. Con la excepción de algún caso muy trivial será necesario pasar a los datos por varios estados intermedios. Pensar a los datos como estados en lugar de cosas nos lleva al segundo concepto: los archivos no son los datos y transformarlos no consiste en modificar un archivo, consiste en generar una cadena de funciones que hacen los cambios de estados. Estas funciones se guardan en un archivo aparte. De este modo nunca haremos cambios irreversibles a los datos o tendremos múltiples versiones de los mismos.

Para analizar datos es necesario disponer de ellos en nuestro entorno de trabajo R y dotarlos de una estructura que comprendamos tanto nosotros como las funciones de R que utilizaremos. Como veremos, en términos técnicos esto significa que trataremos siempre manejarlos como una estructura de la clase data.frame y en formato tidy o prolijo. Esos también deben estar limpios, es decir, estar claramente especificados en su tipo, codificados de manera consistente y libre ambigüedades. En términos prácticos eso significa que las columnas tendrán nombres claros y comprensibles9 y especificado el tipo de datos que contienen –numérico, factor, caracter, fecha, etc-; que el conjunto de datos estará libre de ambigüedades de codificación y errores, incluídos los ortográficos y que los casos perdidos estarán explícitamente señalados como valores NA. La tranformación de datos será mucho más fluida si trabajamos con conjunto de datos limpio, en este sentido de la palabra. Transformar los datos no significa en modo alguno alterarlos, significa estrictamente cambiarles la forma: modificar su estructura, pero no la información que contienen. Es muy probable que una transformación implique también pérdida de información, pero a cambio obtendremos beneficios de inteligibilidad.

En apretada síntesis la manipulación de datos se resume en cuatro operaciones:

  • Extraer subconjuntos de datos. Ya sea subconjuntos de filas o columnas. En los casos prácticos nunca haremos un análisis sobre la totalidad de los datos.
  • Transformarlos. Realizar operaciones aritméticas o lógicas sobre los datos. En general cuando una variable es contínua realizamos operaciones aritméticas, cuando es categórica, lógicas.
  • Obtener sumarios del conjunto de los datos o por grupos. Con frecuencia el análisis no se hace sobre todos los datos sino sobre medidas sumarias: conteos, medias, desviaciones estandar.
  • Unirlos con otros datos. La proliferación de bases de datos hace cada vez más útil combinar múltiples fuentes para enriquecer el análisis.

Este documento se basea en un paradigma de trabajo –la programación funcional basada en la inmutabilidad de los datos y la transparencia referencial–, un conjunto de herramientas disponibles en R –reunidas en las librerías tidyr:: y dplyr:: entre otras– y un formato preferido para datos –tidy data– compatible con ese paradigma y herramientas. Con estos tres pilares podermos llevar a cabo las operaciones resumidas previamente.

4.2 Manipulación de datos con tidyverse::

Las tareas de operaciones de manipulación de datos que hemos mencionado pueden llevarse a cabo de distintas maneras. La librería base:: de R contiene operadores y funciones para hacerlo, por ejemplo [,] para extraer subconjuntos, subset() para operaciones agrupadas, merge(), cbind() o rbind() para combinar múltiples fuentes de datos. A pesar de ser funciones sumamente flexibles y aplicables a múltiples estructuras de datos no son las más convenientes. Están pensadas para usarlas en en un paradigma procedimental, más que con uno funcional, además generan un código dificil de leer y nos obligan a repetir los nombres de las estructuras de datos en cada llamada. La librería dplyr:: ofrece un conjunto unificado de herramientas de manipulación de datos que induce a la programación funcional, produce código legible cuya comprensión es intuitiva y, al estar implementada en lenguaje C, ofrece tiempos de ejecución muy cortos. El conjunto de herramientas de dplyr:: funciona exclusivamente con la estructura de datos data.frame. Esta estrutcuta no es tan rápida como una matríz para operaciones aritméticas ni tan flexibles como una lista, pero es mucho más fácil de manejar: las columnas son las variables y las filas las observaciones. Una ventaja aún mayor es que un data.frame siempre es un data.frame. Es mucho más fácil organizar los procesos si sabemos exactamente qué entra y qué sale. Las funciones de dplyr:: sólo admiten como imput un data.frame y siempre producen como output un data.frame o un mensaje de error. Esta estabilidad de estructura hace que nuestro código se comporte de una forma predecible y los datos nunca pierdan sus atributos. El output de las funciones es completamente predecible y podemos pasarlo con confianza como input de la siguiente, sin tener que registrarle un nombre en el entorno. Las capacidades de dplyr:: están ampliadas por algunas librerías cómplices. Una importante es magrittr::, que introduce a R el operador binario %>%,10 una tubería a la que leemos en voz alta como “después”. Con %>% enlazamos los pasos de la manipulación de datos de las funciones de dplyr:: en el orden natural de ejecución. Con %>% organizamos una secuencia de análisis que culminará en un gráfico así: importar_datos %>% recodificar %>% hacer_conteos %>% hacer_grafico. Es decir, leer datos de un archivo, después recodificar esos datos, después hacer conteos sobre los datos recodificados y después graficar esos conteos.
dplyr:: importa el operador %>% de magrittr::, así que lo tendremos siempre disponible. Si queremos usar los restantes operadores deberemos cargar la librería.11
Otra librería hermana de dplyr:: es tidyr::, que incluye funciones para corregir algunos errores frecuentes en bases de datos y cambiarles la estrctura. tidyr:: además introduce el concepto datos prolijos o tidy data, una manera consistente de organizar la información contenida en estructura de la clase data.frame que facilita su manipulación. Ya veremos de qué se trata y por qué son importantes. Dado que dplyr:: funciona mejor con datos que tienen cierto formato el primer paso será identificar cuál es ese formato de datos.

4.3 La forma de los datos.

4.3.1 ¿Sumarios de datos o base de datos?

Con frecuencia los datos que encotramos en internet no son bases de datos en sentido estricto, sino sumarios o informes que condensan información. Una tabla en la que se registran cada una de las ventas de una frutería, con montos, cantidades, fecha y hora de la transacción, es una base de datos en bruto. Una tabla que resume las ventas mensuales es un sumario. Es muy probable que ese sumario se haya originado en una base de datos, pero esta o no es de acceso público o debemos seguir buscando para encontrarla. Siempre que resulte posible trabajaremos con bases de datos tan desagregadas como nos resulte posible conseguir, ya que tienen mayor cantidad de información. Si es necesario un sumario podemos realizarlo, pero no a la inversa. Es decir, a partir de una base de datos podemos crear los sumarios, pero desde los sumarios no podemos recrear la base de datos.

Table 4.1: Base datos cruda
Fecha Producto Precio Cantidad
20/02/2017 Manzana 10 1.0
20/02/2017 Pera 15 2.0
21/03/2017 Ciruela 13 0.5
22/03/2017 Naranja 9 3.0
Table 4.1: Sumario de datos
Mes Ventas
Febrero 40.0
Marzo 33.5

En R y con dplyr:: podemos manejar información en versión sumario, cosa que haremos cuando no podemos acceder a los datos crudos. Sin embargo como dplyr:: funciona solamente con data.frames es necesario que esos datos tengan una estructura rectangular.

4.4 Datos rectangulares.

Con dplyr:: podemos manipular datos provenientes importados desde casi cualquier formato de archivo, pero si como trabajamos con la estructura data.frame es necesario que cumplan una condición: los datos deben ser rectangulares. Por rectangulares se entiende que están organizados en filas y columnas contíguas y que cada filas tiene el mismo largo que las demás, así como todas las columnas.12 Cuando la intersección de una fila y una columna no tiene un dato válido debe codificarse como NA, not available o información perdida.

Es frecuente que cuando descargamos datos capturados o procesados con Excel los datos no sean rectangulares. Es un práctica tan mala como ampliamente difundida entre los usuarios de Excel usar la misma hoja para alojar los datos y el procesamiento de datos.13 o aprovechar la flexibilidad de esa aplicación para poner datos que corresponden a diferentes temáticas o indicadores en la misma columna. El proceso de importar esos datos mal formateados a R es penoso.

Veamos un ejemplo de datos no rectangulares y rectangulares.

Table 4.2: Datos no rectangulares
Ventas X__1 X__2 X__3 X__4
Frutería “La desprolija” NA NA NA NA
Primer Trimestre NA NA NA NA
Manzanas 100 NA NA NA
Peras 120 NA Ventas de fruta de carozo: 614
Ciruelas 85 NA NA NA
Segundo Trimestre NA NA Ventas de frutas de pepita: 166
Manzanas 110 NA NA NA
Peras 40 NA NA NA
Ciruelas 25 NA NA NA
Tercer Trimestre NA NA NA NA
Manzanas 60 NA NA NA
Peras 45 NA NA NA
Ciruelas 22 NA NA NA
Cuatro Trimestre NA NA NA NA
Manzanas 48 NA NA NA
Peras 91 NA NA NA
Ciruelas 34 NA NA NA
NA NA NA NA NA
Ventas totales en el año: NA 780 NA NA
Table 4.2: Datos rectangulares
Fruta Primer trimestre Segundo Trimestre Tercer Trimestre Cuatro Trimestre
Manzanas 100 110 60 48
Peras 120 40 45 91
Ciruelas 85 25 22 34

Los datos no rectangulares fueron creados en Excel y R los fuerza a formato rectangular agregando NA allí donde es necesario. Sería muy dificultoso manipular esos datos desde R. Como en cada columna puede haber más de un tipo de dato (ejp. la columna 1 tiene información sobre frutas y sobre trimestres) o ninguno no hay forma de llamarlas por nombre. Si eso fuera poco un sumario de datos (ventas de frutas de carozo y pepita) comparte el espacio con datos en bruto.

En la estructura rectangular están solamente los datos y podemos manipularlos con facilidad. La sumatoria de la columna 2 nos da las ventas totales del primer trimestre. La sumatoria de la fila 1 las ventas anuales de Manzanas. No tiene sumarios, pero podríamos generarlos con mucha gran facilidad.

Si importamos datos desde Excel debemos prestar mucha atención a que estén en formato rectangular. Si el formato fuera irregular la mejor alternativa es pasarlos a formato rectangular usando el mismo Excel, antes de imporarlos a R. Cargue todos los datos, si es necesario en varias estructuras pequeñas, cada una de las cuales deberá ser rectangular. No se preocupe por los sumarios que dependan únicamente de los datos incluídos en la base o bases, con datos bien estructurados reconstruirlos lleva segundos.

Guarde su información en formato rectangular siempre, aún cuando no tenga planeado usar R. Antes de ingresar datos a una planilla de cálculos piense primero: ¿Qué operaciones voy a realizar sobre estos datos? ¿Cuál es la mejor forma de organizarlos?

4.4.1 Datos prolijos (tidy data)

Los datos prolijos son aquellos en los que se cumplen simultaneamente dos condiciones: cada columna es una variable y cada fila una observación. Quizás un ejemplo nos aclare el problema. Veamos primero un conjunto de datos que parece muy razonalbe, pero que de acuerdo con nuestra definición no está en un formato prolijo:

Table 4.3: Datos desprolijos
Fruta Indicador 2015 2016
Mandarina Precio 10 12
Toronja Precio 14 15

¿Por qué son desprolijos estos datos? Porque Precio no es una observación sino una variable y los años no son variables, son puntos de datos u observaciones. En formato prolijo deberíamos tener las columnas Fruta, Año y Precio, con una observación por cada año y fruta.14

En versión prolija sería así:

Table 4.4: Datos prolijos
Fruta Año Precio
Mandarina 2015 10
Mandarina 2016 12
Toronja 2016 14
Toronja 2016 15

Siempre que generemos datos –o estemos en condiciones de especificar el formato que tendrán– elegiremos datos prolijos. Si no podemos obtenerles en ese formato entonces los reformatearemos hasta llevarlos a datos prolijos. La librería tidyr:: incluye funciones que solucionan muchos de los problemas frecuentes para pasar datos desprolijos a prolijos.

4.4.2 Reformateo de datos.

De ningún modo vamos a hacer ese reformateado de datos manualmente, un proceso tedioso y propenso a errores. tidyr:: tiene la función gather() que se especializa en solucionar este problema.15 gather() toma un conjunto de datos con las observaciones en las colunas, convierte a cada una de esas columnas en una clave y crea otra nueva que registra el valor correspondiente a cada. Es decir, nos regresa la versión prolija de nuestros datos.

## # A tibble: 2 x 4
##   Fruta     Indicador `2015` `2016`
##   <chr>     <chr>      <dbl>  <dbl>
## 1 Mandarina Precio        10     12
## 2 Toronja   Precio        14     15
## # A tibble: 8 x 2
##   key       value    
##   <chr>     <chr>    
## 1 Fruta     Mandarina
## 2 Fruta     Toronja  
## 3 Indicador Precio   
## 4 Indicador Precio   
## 5 2015      10       
## 6 2015      14       
## 7 2016      12       
## 8 2016      15
## # A tibble: 4 x 4
##   Fruta     Indicador key   value
##   <chr>     <chr>     <chr> <dbl>
## 1 Mandarina Precio    2015     10
## 2 Toronja   Precio    2015     14
## 3 Mandarina Precio    2016     12
## 4 Toronja   Precio    2016     15
## # A tibble: 4 x 3
##   Fruta     Año   Precio
##   <chr>     <chr>  <dbl>
## 1 Mandarina 2015      10
## 2 Toronja   2015      14
## 3 Mandarina 2016      12
## 4 Toronja   2016      15
## # A tibble: 4 x 3
##   Fruta     Año   Precio
##   <chr>     <chr>  <dbl>
## 1 Mandarina 2015      10
## 2 Toronja   2015      14
## 3 Mandarina 2016      12
## 4 Toronja   2016      15

4.5 Manejo de datos con dplyr::

Con los datos cargados y en formato prolijo manipularlos con dplyr() es muy fácil. Quizás lo más dificil sea figurarnos el estado de los datos al que queremos llegar. Una vez que tenemos una idea clara del punto de partida y el punto de llegada debemos dividir el trayecto en pasos simples, tan simples como para ser comprensibles por R y menlazar esos pasos con el operador %>%. Si partimos de los datos en la tabla “Datos prolijos” y queremos obtener un promedio de ventas anuales de los dos productos primero deberíamos cargar los datos, luego agruparlos por año y obtener la media por grupos e imprimirla para hacerla visible. Con dplyr lo haríamos así: datos_prolijos %>% group_by(Año) %>% summarise(mean(Precio)). Con esta simple estructura de sintaxis podemos hacer prácticamente cualquier manipulación de datos.

4.5.1 Verbos básicos de dplyr::

La manipulación de datos con dplyr:: se basa en 5 verbos básicos.

  • select(), para seleccionar columnas. Si el formato es prolijo columna y variables son equivalentes.
  • filter(), para filtrar filas de acuerdo a una o más condiciones.
  • group_by(), para generar grupos. Admite más de un nivel de agrupamiento.
  • mutate(), para hacer transformaciones y recodificación de variables. Regresa un resultado por fila.
  • summarise(), para generar sumarios de variables. Regresa un resultado por variable o por cada grupo previamente definido con group_by().
  • El operador %>% nos permite encadenar operaciones. %>% pasa el output de una función como primer argumento de la siguiente. Normalmente el primer argumento de una función son los datos, con lo que nos ahorraremos tipear una y otra vez a que datos nos referimos.

A estos verbos básicos se agregan otros de uso menos frecuente, pero de gran utilidad en ciertas ocasiones.

  • arrange(), para ordenar resultados en orden numérico o alfabético.
  • recode(), para recodificar variables. Se lleva muy bien con mutate().
  • mutate_all(), mutate_if() y mutate_at(), para hacer transformaciones a varias columnas de una vez. Técnicamente vectoriza una función de transformación.
  • spread() y gather() para reformatear nuestra estructura de datos y pasar de formato largo a ancho y de ancho a largo. Pertenecen a tidyr(), una librería hermana de dplyr::
  • rename() para cambiar nombres de columna.
  • La familia de funciones _join para combinar diferentes datos en una misma estuctura. La sintaxis es algo compleja, pero tiene muchísima flexibilidad.

4.5.2 Uso de la de sintaxis de dplyr::

Repasaremos algunas funciones básicas de dplyr::. Produciremos intencionalmente algunos errores que aclararán el proceso. Se presenta la sintaxis paso por paso, con la salida en consola correspondiente a cada paso. Buena parte del código es redundante, sin embargo se lo incluye como ejemplo del flujo de trabajo típico con dplyr:: y magrittr::: hacemos una operación, verificamos el resultado, luego encadenamos la siguiente, verificamos y así hasta obtener el resultado esperado.

## # A tibble: 6 x 3
##   Col1    Col2       Col3
##   <chr>   <chr>     <dbl>
## 1 Pepita  Manzana      48
## 2 Pepita  Pera         52
## 3 Cítrico Naranja      12
## 4 Cítrico Mandarina     8
## 5 Carozo  Durazno      60
## 6 Carozo  Ciruela      55
## # A tibble: 6 x 3
##   Tipo    Fruta     Precio
##   <chr>   <chr>      <dbl>
## 1 Pepita  Manzana       48
## 2 Pepita  Pera          52
## 3 Cítrico Naranja       12
## 4 Cítrico Mandarina      8
## 5 Carozo  Durazno       60
## 6 Carozo  Ciruela       55
## Error in filter_impl(.data, quo): Evaluation error: objeto 'Col2' no encontrado.
## # A tibble: 2 x 3
##   Tipo    Fruta     Precio
##   <chr>   <chr>      <dbl>
## 1 Cítrico Naranja       12
## 2 Cítrico Mandarina      8
## # A tibble: 4 x 3
##   Tipo   Fruta   Precio
##   <chr>  <chr>    <dbl>
## 1 Pepita Manzana     48
## 2 Pepita Pera        52
## 3 Carozo Durazno     60
## 4 Carozo Ciruela     55
## # A tibble: 5 x 3
##   Tipo    Fruta   Precio
##   <chr>   <chr>    <dbl>
## 1 Pepita  Manzana     48
## 2 Pepita  Pera        52
## 3 Cítrico Naranja     12
## 4 Carozo  Durazno     60
## 5 Carozo  Ciruela     55
## # A tibble: 4 x 2
##   Precio Fruta  
##    <dbl> <chr>  
## 1     48 Manzana
## 2     52 Pera   
## 3     60 Durazno
## 4     55 Ciruela
## # A tibble: 3 x 2
##   Tipo    promedio
##   <chr>      <dbl>
## 1 Cítrico     10  
## 2 Pepita      50  
## 3 Carozo      57.5
## # A tibble: 6 x 5
##   Tipo    Fruta         Precio Kilos Capital
##   <chr>   <chr>          <dbl> <dbl>   <dbl>
## 1 Pepita  Manzana Verde     48    12     576
## 2 Pepita  Pera              52     7     364
## 3 Cítrico Naranja           12    50     600
## 4 Cítrico Mandarina          8    40     320
## 5 Carozo  Durazno           60     3     180
## 6 Carozo  Ciruela           55    10     550

4.6 Uso avanzado de dplyr::

4.6.1 Alternar entre formato largo y ancho.

El formato de datos largo es el que llamamos prolijo. Sin embargo en ocasiones puede ser necesario hacer el proceso inverso y pasar datos de formato largo a formato ancho. Por ejemplo, para hacer operaciones matemáticas entre columnas. Siempre es mejor partir del formato largo y prolijo y pasar a formato ancho allí donde es necesario. La función spread() hace este cambio.

## # A tibble: 2 x 3
##   Fruta     `2015` `2016`
##   <chr>      <dbl>  <dbl>
## 1 Mandarina     10     12
## 2 Toronja       14     15
## # A tibble: 2 x 4
##   Fruta     `2015` `2016` variación_precio
##   <chr>      <dbl>  <dbl>            <dbl>
## 1 Mandarina     10     12                2
## 2 Toronja       14     15                1

4.6.2 Seleccionar las columnas que cumplen determinada condición.

Hasta ahora hemos visto como seleccionar columnas escribiendo sus nombres separados por comas o usando - para señalar cuales no queremos que permanezcan. select() tiene algunas funciones ayudantes que permiten seleccionar columnas de acuerdo con alguna condición lógica y pueden ser de gran ayuda cuando trabajamos con bases de datos con gran número de columna.

## # A tibble: 1 x 2
##   vegetalcalabacin vegetalzanahoria
##              <dbl>            <dbl>
## 1               15               10
## # A tibble: 1 x 2
##   frutamanzana frutamandarina
##          <dbl>          <dbl>
## 1           10              8
## # A tibble: 1 x 3
##   frutamanzana frutamandarina vegetalzanahoria
##          <dbl>          <dbl>            <dbl>
## 1           10              8               10
## # A tibble: 1 x 3
##   frutamandarina vegetalcalabacin vegetalzanahoria
##            <dbl>            <dbl>            <dbl>
## 1              8               15               10

4.6.3 Filtrar por más de una condición o dentro de un conjunto.

Filter es una herramienta muy potente para hacer subconjuntos de datos. Para sacar el mayor provecho vale la pena reflexionar sobre la forma en que opera y la sintaxis de la función nos da una pista. Entre los paréntesis posteriores a filter ubicamos una condición lógica que especificamos a través de operadores binarios. Los operadores binarios más conocidos son los que usamos frecuentemente para definir operaciones aritméticas: + para sumar o - para restar. Se los llama binarios porque se ubican entre dos expresiones y establecen una relación entre ellas, de lo contrario sería operadores unarios, otra clase también definida por R. Consiguientemente si no ubicamos al operador binario entre dos expresiones R nos regresará un error. A las dos expresiones que envuelven a un operador binario las llamados lado derecho y lado izquierdo. Esto es de la mayor importancia, ya que la ubicación en cada uno de los lados hace que la operación sea diferente. La aritmética nos ayuda una vez más a comprenderlo, si queremos hacer una resta entre los números 10 y 2 no obtenemos el mismo resultado alternando el lado en que los ubicamos. 10-2 no es lo mismo que 2-10. a %in% x, que se lee en voz alta como ‘a pertenece a x’ no es lo mismo que ‘x pertenece a a’. Filter utiliza todos los operadores binarios de R, que se detallan en tabla a continuación. Con esta especificación R evalúa el cumplimiento de una condición y regresa TRUE cuando se cumple y FALSE cuando no. Dado que R opera por defecto de manera vectorizada, cuando especificamos un vector evalúa todo el vector y regresa un vector de TRUEy FALSE del mismo largo del que introduducimos. Posteriormente filter() conseva solamente aquellas filas en las que el resultado de la evaluación fue TRUE. Esta evaluación aplica tanto para cadenas de caracteres como para datos del tipo numérico. En el caso de las cadenas de caracteres algunos operadores utilizarán el orden alfabético, así "pera">"manzana" regresa TRUE, porque p ocupa el lugar 16 en el alfabeto y m el 13. En caso de empate R evaluará la segunda letra y así hasta desempatar.
Table: Operadores binarios de R disponibles para filter()

Operador Uso
== Igual que
> Mayor que
>= Mayor o igual que
< Menor que
<= Menor o igual que
%in% | Pertenece a un vector|Vectores numéricos o de caracteres&| Y lógica, para especificar una segunda condición a cumplirse | Entre dos expresiones binarias | Ó lógica, para especificar una condición alternativa | Entre dos expresiones binarias!| No, invierte el sentido de cada operador, regresa TRUE cuando *no* se cumple la condición | Detrás de cualquiera de los operadores%like%`

Usando estos operadores y sus combinaciones podemos hacer prácticamente cualquier operación de filtrado de filas, empleando información de una o más columnas, siempre que estén dentro del data.frame al que estamos manipulando. Si bien es posible hacer filtrados sucesivos encadenando operaciones de filter() por cuestiones de desempeño –sobre todo en bases de datos muy grandes– y compacitud del código es preferible cargar tantas condiciones como es posible en la misma cadena. Recuerde que cada vez que invocamos la función R debe recorrer todo el vector evaluando, es mejor que lo haga sólo una vez para un conjunto de condiciones complejas que muchas veces para condiciones simples.

## 
## Attaching package: 'data.table'
## The following objects are masked from 'package:dplyr':
## 
##     between, first, last
## The following object is masked from 'package:purrr':
## 
##     transpose
## # A tibble: 2 x 3
##   Estado     Municipio Población
##   <chr>      <chr>         <dbl>
## 1 Nuevo León Juárez       333481
## 2 Chiapas    Juárez        21222
## # A tibble: 3 x 3
##   Estado     Municipio    Población
##   <chr>      <chr>            <dbl>
## 1 Nuevo León Juárez          333481
## 2 Chiapas    Juárez           21222
## 3 Chiapas    Unión Juárez     15350
## # A tibble: 4 x 3
##   Estado           Municipio  Población
##   <chr>            <chr>          <dbl>
## 1 Chihuahua        Juárez       1391180
## 2 Nuevo León       Juárez        333481
## 3 Chiapas          Juárez         21222
## 4 Ciudad de México Milpa Alta    137927
## # A tibble: 1 x 3
##   Estado   Municipio          Población
##   <chr>    <chr>                  <dbl>
## 1 Guerrero Acapulco de Juárez    810669
## # A tibble: 2 x 3
##   Estado           Municipio          Población
##   <chr>            <chr>                  <dbl>
## 1 Guerrero         Acapulco de Juárez    810669
## 2 Ciudad de México Milpa Alta            137927

4.6.4 Transformacion avanzada de datos.

Usándolo con cuidado mutate() es una herramienta muy potente para hacer transformaciones de datos. En términos muy prácticos mutate() une un vector resultado de una función al data.frame con el que estamos trabajando. Es decir, cualquier función que tome uno o más vectores y nos regrese otro puede utilizarse dentro de mutate(), incluyendo algunas básicas como ifelse() para operaciones condicionales vectoriales, cumsum() para sumas acumuladas. lag() y lead() para mover un vector una línea abajo o hacia arriba respectivamente, permitiéndonos computar la diferencia entre una fila y la anterior o posterior. También es posible pasar varias transformaciones al mismo tiempo separándolas con comas. La familia ampliada de mutate() incluye mutate_all(), para aplicar la misma transformación a todas las variables, mutate_if() que aplica una transformación a las variables que cumplen con una condición.

## # A tibble: 9 x 4
##   Estado           Municipio          Población tamaño      
##   <chr>            <chr>                  <dbl> <chr>       
## 1 Chihuahua        Juárez               1391180 Muy poblado 
## 2 Nuevo León       Juárez                333481 Poco poblado
## 3 Chiapas          Juárez                 21222 Poco poblado
## 4 Chiapas          Unión Juárez           15350 Poco poblado
## 5 Guerrero         Acapulco de Juárez    810669 Muy poblado 
## 6 Ciudad de México Milpa Alta            137927 Poco poblado
## 7 Chihuahua        Batopilas               9751 Poco poblado
## 8 Nuevo León       Apodaca               115913 Poco poblado
## 9 Nuevo León       Carmen                  4906 Poco poblado
## # A tibble: 9 x 5
##   Estado           Municipio          Población acumulado diferencia
##   <chr>            <chr>                  <dbl>     <dbl>      <dbl>
## 1 Chihuahua        Juárez               1391180   1391180         NA
## 2 Nuevo León       Juárez                333481   1724661   -1057699
## 3 Chiapas          Juárez                 21222   1745883    -312259
## 4 Chiapas          Unión Juárez           15350   1761233      -5872
## 5 Guerrero         Acapulco de Juárez    810669   2571902     795319
## 6 Ciudad de México Milpa Alta            137927   2709829    -672742
## 7 Chihuahua        Batopilas               9751   2719580    -128176
## 8 Nuevo León       Apodaca               115913   2835493     106162
## 9 Nuevo León       Carmen                  4906   2840399    -111007
## # A tibble: 9 x 5
##   Estado           Municipio          Población   acumulado   diferencia  
##   <chr>            <chr>              <chr>       <chr>       <chr>       
## 1 Chihuahua        Juárez             Son 139118… Son 139118… Son NA pers…
## 2 Nuevo León       Juárez             Son 333481… Son 172466… Son -105769…
## 3 Chiapas          Juárez             Son 21222 … Son 174588… Son -312259…
## 4 Chiapas          Unión Juárez       Son 15350 … Son 176123… Son -5872 p…
## 5 Guerrero         Acapulco de Juárez Son 810669… Son 257190… Son 795319 …
## 6 Ciudad de México Milpa Alta         Son 137927… Son 270982… Son -672742…
## 7 Chihuahua        Batopilas          Son 9751 p… Son 271958… Son -128176…
## 8 Nuevo León       Apodaca            Son 115913… Son 283549… Son 106162 …
## 9 Nuevo León       Carmen             Son 4906 p… Son 284039… Son -111007…
## # A tibble: 9 x 3
##   Estado           Municipio          Población
##   <chr>            <chr>              <chr>    
## 1 Chihuahua        Juárez             1391180  
## 2 Nuevo León       Juárez             333481   
## 3 Chiapas          Juárez             21222    
## 4 Chiapas          Unión Juárez       15350    
## 5 Guerrero         Acapulco de Juárez 810669   
## 6 Ciudad de México Milpa Alta         137927   
## 7 Chihuahua        Batopilas          9751     
## 8 Nuevo León       Apodaca            115913   
## 9 Nuevo León       Carmen             4906

4.6.5 Sumarios avanzados.

summarise() nos permite crear sumarios y es especialmente útil con datos agrupados. Sin embargo es posible que no exista una función que produzca el sumario que necesitamos. En ese caso podemos pasar a summarise() una función personalizada, ya sea una función que hemos definido previamente y hemos asignado nombre o una función anónima o función lambda. En este caso estimaremos la media de población para nuestra muestra, el desvío estandar y el error estandar de la media. Crearemos una función para calcular el error estándar traduciendo a R la notación matemática del error estándar: \(SE\hat{x}=\frac{\sigma}{\sqrt{n}}\), el error estándar de la media es igual al desvío estándar entre la raíz cuadrada de n.

## # A tibble: 1 x 4
##       n   media  desvio error_estandar
##   <int>   <dbl>   <dbl>          <dbl>
## 1     9 315600. 479663.        159888.
## # A tibble: 1 x 4
##       n   media  desvio error_estandar
##   <int>   <dbl>   <dbl>          <dbl>
## 1     9 315600. 479663.        159888.
## # A tibble: 5 x 5
##   Estado               n   media  desvio error_estandar
##   <chr>            <int>   <dbl>   <dbl>          <dbl>
## 1 Chiapas              2  18286    4152.          2936.
## 2 Chihuahua            2 700466. 976818.        690714.
## 3 Ciudad de México     1 137927      NA            NaN 
## 4 Guerrero             1 810669      NA            NaN 
## 5 Nuevo León           3 151433. 167143.         96500.

4.6.6 Funciones avanzadas de combinación de bases de datos.

dplyr:: nos permite tiene algunos verbos muy usuales en el software de manejo de bases de datos que sirven para combinar múltiples fuentes de datos: los joins o uniones. Sin la sintaxis complicada de un lengujae como SQL podemos combinar bases de datos de manera flexible y aprovechar múltiples fuentes de datos, siempre que tengan al menos una columna que coincida. Podríamos usarlo para unir dos bases de datos con la misma unidad de análisis territorial o para combinar estructuras de datos asimétricas en cuanto al largo.

## # A tibble: 5 x 5
##   Tipo    Fruta   Precio Kilos precio_futuro
##   <chr>   <chr>    <dbl> <dbl>         <dbl>
## 1 Pepita  Manzana     48    12            48
## 2 Pepita  Pera        52     7            52
## 3 Cítrico Naranja     12    50            12
## 4 Carozo  Durazno     60     3            60
## 5 Carozo  Ciruela     55    10            55
## # A tibble: 7 x 5
##   Tipo    Fruta     Precio Kilos precio_futuro
##   <chr>   <chr>      <dbl> <dbl>         <dbl>
## 1 Pepita  Manzana       48    12            48
## 2 Pepita  Pera          52     7            52
## 3 Cítrico Naranja       12    50            12
## 4 Cítrico Mandarina      8    40            NA
## 5 Carozo  Durazno       60     3            60
## 6 Carozo  Ciruela       55    10            55
## 7 <NA>    Toronja       NA    NA             8
## # A tibble: 1 x 4
##   Tipo    Fruta     Precio Kilos
##   <chr>   <chr>      <dbl> <dbl>
## 1 Cítrico Mandarina      8    40
## # A tibble: 1 x 2
##   Fruta   precio_futuro
##   <chr>           <dbl>
## 1 Toronja             8
## # A tibble: 6 x 5
##   Tipo    Fruta     Precio Kilos precio_futuro
##   <chr>   <chr>      <dbl> <dbl>         <dbl>
## 1 Pepita  Manzana       48    12            48
## 2 Pepita  Pera          52     7            52
## 3 Cítrico Naranja       12    50            12
## 4 Cítrico Mandarina      8    40            NA
## 5 Carozo  Durazno       60     3            60
## 6 Carozo  Ciruela       55    10            55

4.6.7 Operadores avanzados de magrittr::

Ya hemos utilizado el principal operador de magrittr::, la tubería %>% que estádisponible directamente en dplyr::. Entender el funcionamiento de %>% puede ayudarnos a conocer sus límites y buscar alternativas para solucionar algunos problemas. %>% es un operador binario, es decir, relaciona un lado izquierdo y un lado derecho. La expresión que está del lado derecho pasa su output a la del lado izquierdo. R no contempla un método específico para pasar los datos de una función a la siguiente, pero el autor de magrittr:: encontró una manera ingeniosa. Dado que la mayoría de las funciones toma a los datos como primera argumento %>% se encarga de “reescribir” la función del lado izquierdo, de manera el primer argumento sean los datos que produjo el lado derecho de la formula. Esto funciona en la mayoría de los casos, pero podemos tener problemas de la función que estamos utilizando en el lado izquierdo espera algo diferente a los datos como primer argumento. Asi con los modelos lineales que especificamos con lm(), esperan como primer argumento de la función la formula del modelo, no los datos. Para solucionar estos problemas magrittr:: utiliza al signo . (un punto) como “comodín” para los datos y nos permite ubicarlos allí donde la sintaxis de la función del lado izquierdo los requiera. Otro operador avanzado es %T>%, que nos permite hacer una –breve– bifurcación. Cuando lo ubicamos detrás de una función %T>%% hace que esta regrese el lado izquierdo y no el derecho. Así, si queremos hacer visible un resultado intermedio usanda la función print(), que luego pasará a la siguiente función no su output sino el que está a su izquierda. %T>% funciona solamente para dar un salto, no más que eso. A veces no es suficiente, podríamos estar interesados en dar algo de formato a los datos intermedios que queremos imprimir y eso implicaría al menos dos saltos. En ese caso podemos envolver las funciones intermedias con {} y poner el operador unario . al final, de modo que pase los datos de la izquierda de {} a la función siguiente. Dentro de los límites de {} puedo hacer cualquier manipulación y generar cualquier outupt.

Por último el operador %$% pasa al lado derecho una serie de vectores en lugar de la estructura original de los datos –que con frecuencia es un data podría serlo un data.frame–. Esto es especialmente útil cuando del lado derecho tenemos una función que espera vectores, ya que nos ahorra la permanente llamada con $ para especificar el data.frame del que tiene que extraer el vector.

## 
## Attaching package: 'magrittr'
## The following object is masked from 'package:purrr':
## 
##     set_names
## The following object is masked from 'package:tidyr':
## 
##     extract
## # A tibble: 9 x 3
##   Estado           Municipio          Población
##   <chr>            <chr>                  <dbl>
## 1 Chihuahua        Juárez               1391180
## 2 Nuevo León       Juárez                333481
## 3 Chiapas          Juárez                 21222
## 4 Chiapas          Unión Juárez           15350
## 5 Guerrero         Acapulco de Juárez    810669
## 6 Ciudad de México Milpa Alta            137927
## 7 Chihuahua        Batopilas               9751
## 8 Nuevo León       Apodaca               115913
## 9 Nuevo León       Carmen                  4906
## # A tibble: 5 x 2
##   Estado               n
##   <chr>            <int>
## 1 Chiapas              2
## 2 Chihuahua            2
## 3 Ciudad de México     1
## 4 Guerrero             1
## 5 Nuevo León           3
## Warning in summary.lm(.): essentially perfect fit: summary may be
## unreliable
## 
## Call:
## lm(formula = Pob2 ~ Población, data = .)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -9.832e-11 -2.564e-11  2.482e-11  2.540e-11  8.182e-11 
## 
## Coefficients:
##              Estimate Std. Error   t value Pr(>|t|)    
## (Intercept) 1.552e-10  2.683e-11 5.786e+00 0.000673 ***
## Población   2.000e+00  4.865e-17 4.111e+16  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.6e-11 on 7 degrees of freedom
## Multiple R-squared:      1,  Adjusted R-squared:      1 
## F-statistic: 1.69e+33 on 1 and 7 DF,  p-value: < 2.2e-16
## # A tibble: 9 x 3
##   Est              Mun                    Pob
##   <chr>            <chr>                <dbl>
## 1 Chihuahua        Juárez             1391180
## 2 Nuevo León       Juárez              333481
## 3 Chiapas          Juárez               21222
## 4 Chiapas          Unión Juárez         15350
## 5 Guerrero         Acapulco de Juárez  810669
## 6 Ciudad de México Milpa Alta          137927
## 7 Chihuahua        Batopilas             9751
## 8 Nuevo León       Apodaca             115913
## 9 Nuevo León       Carmen                4906
## # A tibble: 9 x 3
##   Estado           Municipio          Población
##   <chr>            <chr>                  <dbl>
## 1 Chihuahua        Juárez               1391180
## 2 Nuevo León       Juárez                333481
## 3 Chiapas          Juárez                 21222
## 4 Chiapas          Unión Juárez           15350
## 5 Guerrero         Acapulco de Juárez    810669
## 6 Ciudad de México Milpa Alta            137927
## 7 Chihuahua        Batopilas               9751
## 8 Nuevo León       Apodaca               115913
## 9 Nuevo León       Carmen                  4906
##                   Municipio
## Estado             Acapulco de Juárez Apodaca Batopilas Carmen Juárez
##   Chiapas                           0       0         0      0      1
##   Chihuahua                         0       0         1      0      1
##   Ciudad de México                  0       0         0      0      0
##   Guerrero                          1       0         0      0      0
##   Nuevo León                        0       1         0      1      1
##                   Municipio
## Estado             Milpa Alta Unión Juárez
##   Chiapas                   0            1
##   Chihuahua                 0            0
##   Ciudad de México          1            0
##   Guerrero                  0            0
##   Nuevo León                0            0
## Warning in chisq.test(.): Chi-squared approximation may be incorrect
## 
##  Pearson's Chi-squared test
## 
## data:  .
## X-squared = 28, df = 24, p-value = 0.26

4.7 Límites de dplyr::

La potencia y simplicidad del abordaje de dplyr:: para la manipulación de datos no hace que esté excento de limitaciones. El primer problema es conceptual: los datos aquí son una entidad abstracta. Lleva algún tiempo acotumbrarse a no tener un registro visual de nuestra materia de trabajo y todavía más a que ni siquiera tengan nombre. Sin embargo armando las cadenas paso a paso podremos ver en consola el output de cada función y tener claro que datos estamos pasando a la función siguiente. Y, en verdad, no tener que llevar registro de los múltiples nombres que nuestros datos pueden adquirir a lo largo del análisis es en realidad gran ventaja. Otros problemas son tecnicos y demandan mucha flexibilidad y creatividad al momento de escribir código. Para mantenernos en el paradigma de programción funcional debemos buscar formas diferentes de lograr los mismo. La elegancia de dplyr:: se debe en gran medida a que se concentra en una sola estructura de datos, el data.frame. Al hacerlo puede ocultar mucha de la complejidad de la manipulación de datos al usuario, conoce la estructura con la que trabaja y puede traducir los comandos simples que le introducimos a comandos mucho más complejos que son los que en realidad ejecuta. Con la elegancia viene una limitación: si necesitamos trabajar con una estructura de datos diferente al data.frame dplyr:: fracasa completamente. Valgan como ejemplo las dificultades para manejar dos versiones de los mismos datos en una misma cadena. dplyr:: está pensado para trabajar con sólo con un conjunto de datos con estructura data.frame –cuando usamos un join estamos conviertiendo a dos conjuntos de datos en uno solo– en busca de un único resultado. Existen maneras de producir y generar el output de resultados intermedios, por ejemplo, usando la tubería %T>% para salidas muy simples o generando una función lambda que encapsule el código de salida y regrese los datos al datos al final.

El mayor problema es lograr que las cadenas de dplyr:: se lleven bien con algunas funciones más antiguas de R, sobre todo aquellas que reciben vectores atómicos como imput o producen listas como output. Esto es especialmente grave porque buena parte del atractivo de R es usar esas funciones específicas e irremplazables. ¿Le interesa el análisis de clases latentes multigrupos con ponderador muestral complejo? La librería LCA lo hace, pero el primer argumento de la función es un objeto de la clase fórmula y el resultado una lista de matrices de cuatro dimensiones, para las que dplyr:: no será de ninugna ayuda. En este y otros casos dplyr:: nos llevará hasta cierto punto, luego no habrá más opción que asignar un nombre al output de la cadena y seguir a pié16. Si esto ocurriera solamente con funciones muy especializadas no sería un problema tan grande, pero ocurre en casos tan comunes como una prueba \(\chi\)2.17 Conocer estos límites será siempre de gran ayuda.

Otro potencial problema es que los métodos de dplyr:: suelen fallar cuando la base de datos no está limpia y adecuadamente codificada, con los casos missing explícitamente señalados y sin errores de ortografía18. Personalmente no creo que esto sea un problema, más bien es una virtud. Dar soluciones ad hoc a los errores de nuestros datos en el momento en el que lo necesitamos es una pésima práctica. Nos garantiza volveremos a encontrar con ese error u otro similar más abajo en el código. Es mejor arreglarlo desde un princio. Todavía mejor es generar una función personalizada que hace los arreglos necesarios e invocarla cada vez que es necesario. De este modo garantizamos la inmutabilidad de los datos. ¿Encontramos un nuevo error que había pasado inadvertido? Solo cambiamos esta función y cuando volvamos a ejecutar el código que la incluye realizará los cambios pertinentes. Un pilar del paradigma de programación funcional es que su entorno de trabajo debería estar poblado de funciones, no de estructuras de datos.

4.8 Manipulación con dplyr::en la práctica. Flujo de trabajo.

En términos muy estilizados el flujo de trabajo del análisis exploratorio de datos sería el siguiente.19

4.8.1 Implementación en dplyr:: de un análisis exploratorio de la base de datos Índice de marginación del CONAPO.

ENT POB_TOT ANALF SPRIM OVSDE OVSEE OVSAE VHAC OVPT PL<5000 IM
Aguascalientes 119322.182 3.742727 16.94182 1.7936364 0.7109091 1.059091 30.56545 0.9800000 64.14273 -0.9220909
Baja California 663153.200 2.290000 11.60800 0.2840000 0.7320000 5.112000 22.80600 1.1980000 17.95800 -1.5100000
Baja California Sur 142405.800 3.286000 14.26400 0.6220000 1.7660000 5.646000 25.77200 3.5420000 20.50800 -1.2734000
Campeche 81811.909 9.765455 24.63182 7.6072727 2.4554545 9.293636 43.98727 4.3109091 51.22636 -0.1338182
Chiapas 44219.559 18.555000 37.32525 3.2210169 2.5353390 14.180254 50.12686 13.1866949 77.97992 0.8246441
Chihuahua 53083.194 7.732687 28.63343 5.5500000 6.3325373 6.109552 24.84925 4.2826866 75.10388 -0.3207761
Coahuila de Zaragoza 77760.921 3.323947 14.95868 1.2457895 0.5836842 2.510000 27.05868 0.7865789 50.04605 -1.1691579
Colima 71123.500 5.338000 19.42100 0.8040000 0.4560000 1.325000 28.11500 2.8980000 37.90100 -1.0235000
Distrito Federal 557415.812 1.484375 6.54125 0.0512500 0.0587500 1.699375 19.61938 0.5768750 1.82750 -1.7696875
Durango 44993.692 5.490513 24.51410 8.1528205 4.3300000 5.350256 28.28538 6.5307692 77.56103 -0.3135128
Guanajuato 127253.848 9.311087 25.26043 6.1306522 1.2017391 5.195870 28.34065 2.5854348 58.49174 -0.5252609
Guerrero 43620.383 20.072346 36.44296 18.7496296 3.5571605 19.495432 47.65679 17.8380247 76.35198 1.1077284
Hidalgo 34028.083 11.103571 23.64464 4.2801190 1.6080952 7.736667 31.16429 3.9871429 76.37321 -0.2994524
Jalisco 62758.640 6.836480 25.36800 3.4060800 1.3576800 2.905440 26.87056 3.0661600 58.44288 -0.7477440
México 129500.864 5.687920 17.20704 4.4409600 0.8722400 5.760800 33.22464 3.2542400 51.59408 -0.7597600
Michoacán de Ocampo 40570.540 11.181416 32.40504 3.7654867 1.2617699 4.832920 31.17097 7.2984071 64.93726 -0.1986372
Morelos 57691.242 6.195455 18.33333 1.7030303 0.5633333 9.861212 31.24424 4.9187879 47.28121 -0.6802424
Nayarit 59052.500 7.631000 23.97050 8.7990000 5.0060000 6.799500 32.67350 6.9410000 63.14500 -0.2349000
Nuevo León 100382.431 3.787059 18.57353 0.9839216 0.7858824 4.066471 28.11275 1.9998039 54.41549 -1.0942157
Oaxaca 6961.209 16.805281 36.09884 2.8206316 3.1497544 11.066702 40.27021 15.8554737 91.27837 0.6180772
Puebla 28428.032 14.312074 32.72539 3.2478802 1.6124885 9.253088 42.44691 8.8613364 76.21313 0.3278249
Querétaro de Arteaga 113242.889 8.568333 21.90611 6.3483333 1.7050000 7.095556 33.48778 2.5894444 72.44111 -0.5086111
Quintana Roo 150156.200 6.969000 18.39200 5.9530000 2.1370000 3.057000 44.57200 4.2250000 36.24100 -0.5632000
San Luis Potosí 46858.966 10.375862 28.86793 4.1108621 3.9877586 18.568103 32.10621 8.2081034 72.41879 0.1196552
Sinaloa 164795.611 6.652778 23.66000 5.4638889 1.3066667 5.844444 34.63333 5.2383333 57.53611 -0.5440556
Sonora 39587.917 3.589583 20.41347 1.8644444 1.9793056 2.133056 24.85278 2.8312500 70.84097 -0.9675694
Tabasco 140898.353 6.646471 20.33588 2.3741176 0.6641176 11.327647 35.55588 4.0582353 63.79412 -0.5448235
Tamaulipas 80039.488 6.232791 25.30000 1.2079070 1.6497674 8.213023 30.23977 3.3969767 61.80233 -0.5246512
Tlaxcala 21214.117 4.319667 13.79917 1.5933333 0.5343333 1.108333 34.21767 2.1665000 48.54050 -0.8518333
Veracruz de Ignacio de la Llave 38266.533 14.142076 33.53835 2.4762736 2.2141038 15.555425 37.42741 8.2850943 70.83278 0.2541981
Yucatán 19784.670 12.498207 32.09783 17.5136792 1.6091509 1.710189 46.18566 2.0950000 70.62226 0.2529906
Zacatecas 27227.741 5.970172 25.48672 4.7017241 0.8882759 3.074483 26.84828 1.6341379 71.13603 -0.6136034

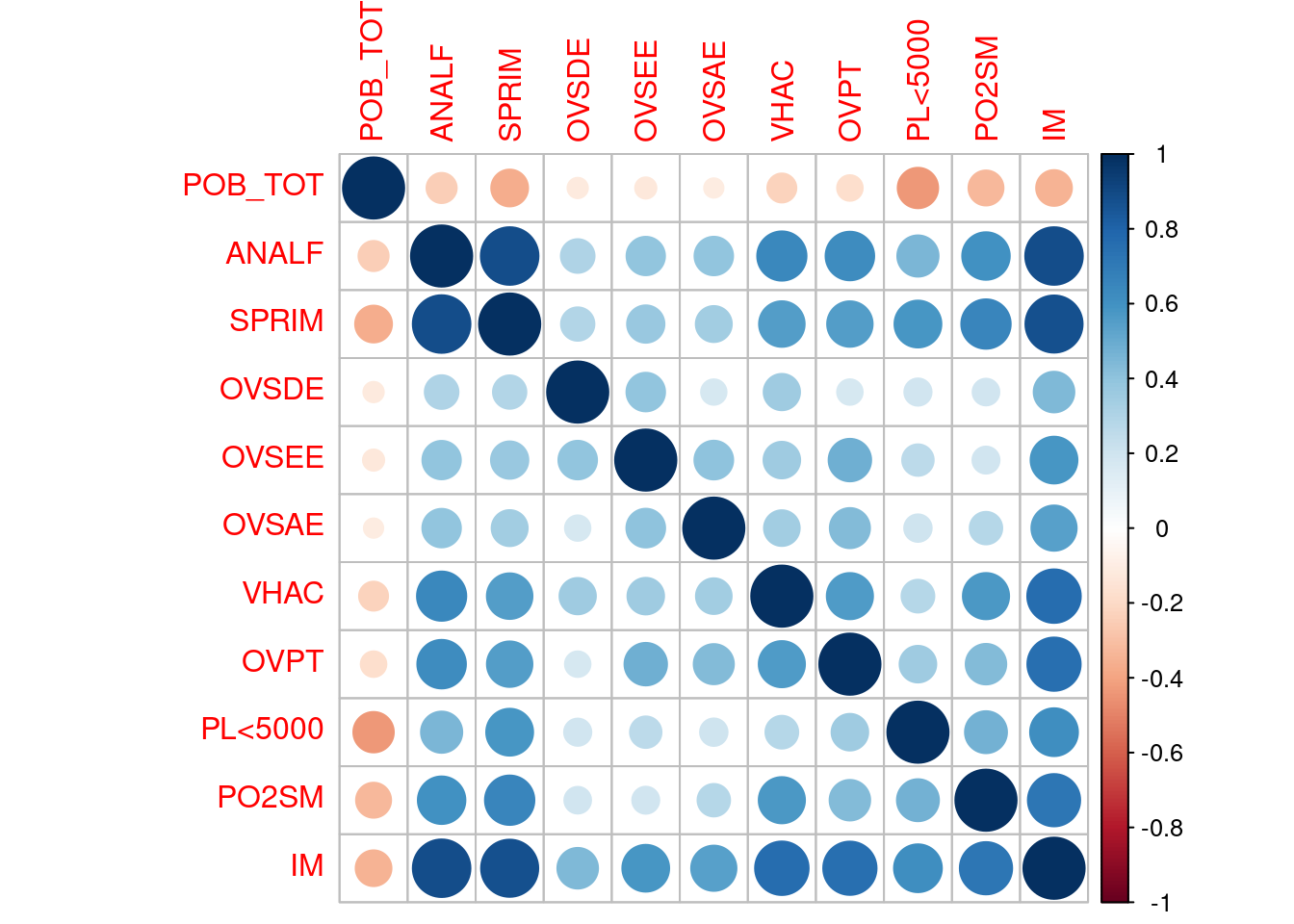
  1. Lamentablemente no podemos hacer lo contrario.↩

  2. Nota para usuarios de Excel. Los datos no son el archivo en el que están los datos. Las estructuras de datos son más bien entidades abstractas que tienen una representación en la memoria y el procesador de nuestra computadora y de la que nos interesan sus atributos. No es necesario –y mucho menos conveniente- modificar un archivo para modificar los datos.↩

  3. Y preferiblemente cortos: en R no seleccionamos las columnas con un menú, introducimos sus nombres en la consola: elija bien esos nombres, los tipeará una y otra vez.↩

  4. Similar en concepto a | de UNIX.↩

  5. Los restantes operadores son %T>%, que hace una bifurcación y para dar output a un paso intermedio y %$>%, que regresa el output como un conjunto de vectores en lugar de un data.frame.↩

  6. Esto no significa que deba tener el mismo número de filas que de columnas, esos serían datos cuadrados, un caso especial de los datos rectangulares.↩

  7. R impide intrínsecamente llevar a caso semejante mala práctica.↩

  8. Si cree que esta desprolijidad se debe a las malas prácticas de la frutería poco sabia en cuestiones de manejo de dato considere que las bases de datos del Banco Mundial suelen tener esta estructura.↩

  9. La sintaxis de gather() puede ser algo complicada, sin embargo una interfaz gráfica llamada tidyshiny() nos puede asistir en el proceso dándonos retroalimentación inmediata. Dado que no está en el repositorio CRAN la instalación es algo más complicada que lo usual, pero puede hacerlo con esta línea que resolverá previamente las dependencia: if(!require(tidyr)) {install.packages("devtools")} ; library(devtools); install_github("MangoTheCat/tidyshiny"). Úsela desde Rstudio en el botón Addins, debajo del menú.↩

  10. Una recomendación en estos casos es remover del entorno el objeto de datos al que asignamos nombre después de utilizarlo. Ya ha cumplido su función, deberíamos descartarlo.↩

  11. chsiq.test() admite una tabla como imput, table() produce tablas, pero recibe vectores como imput.↩

  12. Los errores ortográficos o de estilo en la codificación de una base de datos son un tema menor. Para R “México”, “MEXICO”, “Mexico”, “méxico” son cuatro cadenas de caracteres completamente diferentes.↩

  13. Nótese el énfasis en exploratorio. Este flujo de trabajo no está organizado alrededor de una hipótesis y utiliza poco o nada del conocimiento disponible sobre un tema. Al carecer de estado del arte y de marco de hipótesis no es un proceso de investigación. Está orientado a familizarizarnos con los datos, identificar y visualizar patrones y relaciones y, en el mejor de los casos, generar nuevas hipótesis. Dicho sea de paso, ni R ni ninguna plataforma de software producen buena investigación o análisis lúcidos, use dplyr, R base o papel y lápiz. A lo sumo pueden facilitarnos los aspectos técnicos y dejarnos más tiempo disponible para investigar o analizar.↩